想獲得更多四川公務(wù)員備考咨詢,歡迎關(guān)注官方微信號:htgwy01
行測備考技巧八 邏輯判斷之必然性推理
邏輯判斷是公務(wù)員考試中的必考題型,主要考查考生對邏輯知識的理解、分析、綜合、判斷、推理能力。從近幾年四川公務(wù)員考試真題來看,邏輯判斷題的題量在8-9題左右,考查內(nèi)容一般分為必然性推理和可能性推理兩個方面。其中,必然性推理是指從題目所給的前提條件必然能推出選項結(jié)論的命題。
許多初次接觸邏輯判斷題的考試,往往糾結(jié)于題目和選項的字面意思,發(fā)現(xiàn)怎么選都選不對,甚至?xí)较朐胶浚聦嵣希@是落入了做題的誤區(qū)。邏輯題考查的并不是考生的閱讀理解能力,而是抽象推理能力,因此,考生應(yīng)把題目抽象成一定的邏輯關(guān)系,并按照邏輯推理的思路解題。下面,途途君就為大家總結(jié)一些必然性推理題中的命題形式和推理方法,供大家參考。
一、直言命題
(1)直言命題概念間的關(guān)系
直言命題,也稱簡單命題,是斷定對象是否具有某種性質(zhì)的單句。如“我們都是中國人”就是一個之言命題。其中,“我們”稱為命題的主項;“中國人”稱為命題的謂項;“都”稱為命題的量項,“是”稱為命題的聯(lián)項。
判斷一個命題的真假,主要看該命題是否與客觀實際相符合,如果與客觀實際相符合,則命題為真,如“小學(xué)生都是學(xué)生”;若與客觀事實不相符,則命題為假,如“小孩子都是學(xué)生”。直言命題的真假是由主項和謂項在外延上所存在的關(guān)系決定的,具體如下表所示:
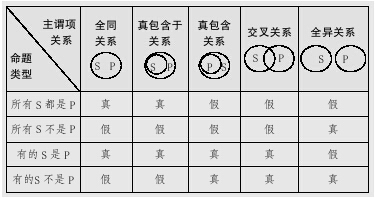
(2)直言命題的對當(dāng)關(guān)系
直言命題的對當(dāng)關(guān)系即不同直言命題之間在真假方面所存在的制約關(guān)系。
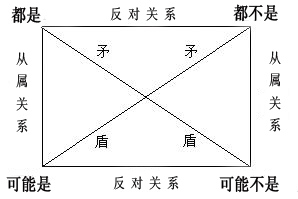
以上圖片中的關(guān)系可以解釋為:
“所有A都是B”與“有的A可能不是B”、“所有A都不是B”與“有的A可能是B”是矛盾關(guān)系,它們中必有一真一假。
“所有A都是B”與“所有A都不是B”是上反對關(guān)系,它們中必有一假,可以同為假。
“有的A可能是B”與“有的A可能不是B”是下反對關(guān)系,它們中必有一真,可以同為真。
“有的A可能是B”包含于“所有A都是B”,可以由“所有A都是B推出”;“有的A可能不是B”包含于“所有A都不是B”,可以由“所有A都不是B”推出。
(3)直言命題的變形推理
直言命題的變形推理就是通過改變前提中直言命題的聯(lián)項或主項與謂項的位置,從而推出結(jié)論的推理。包括換位推理與換質(zhì)推理。
1、換位推理
換位推理即通常所說的“倒過來說”,就是通過改變前提中直言命題的主項和謂項的位置,從而得出結(jié)論的推理方法。
“所有A是B”可以換位為“有些B是A”,如:所有蘋果是水果→有些水果是蘋果;
“所有A不是B”可以換位為“所有B不是A”,如:所有蘋果不是香蕉→所有香蕉不是蘋果;
“有些A不是B”可以換位為“有些B是A”,如:有些學(xué)生是黨員→有些黨員是學(xué)生;
“有些A不是B”無法進(jìn)行換位,如:有些學(xué)生不是黨員不能換位成有些黨員不是學(xué)生。
2、換質(zhì)推理
換質(zhì)推理即通常所說的“換一個說法”,就是通過改變前提中直言命題的聯(lián)項,從而推出結(jié)論的推理方法。
“所有A是B”可以換質(zhì)為“所有A不是非B”,如:所有文字都是有意義的→所有文字不是沒有意義的;
“所有A不是B”可以換質(zhì)為“所有A是非B”,如:所有人都不是完美的→所有人都是不完美的;
“有的A是B”可以換為“有的A不是非B”,如:有的嫌疑人是有罪的→有的嫌疑人不是沒有罪的;
“有的A不是B”可以換為“有的A是非B”,如:有的嫌疑人不是有罪的→有的嫌疑人是沒有罪的。
二、三段論推理
三段論推理是由兩個直言命題作為前提和一個直言命題作為結(jié)論而構(gòu)成的推理。其中兩個前提中包含有三個不同的概念,且在前提和結(jié)論中,每個概念都出現(xiàn)兩次。例如:所有的糖都是甜的,棒棒糖是糖,所以棒棒糖是甜的。
三段論推理需要遵循一定的規(guī)則,常用的有以下兩種規(guī)則:
(1)一特則特:兩個前提不能都是特稱命題,且只要前提有一個為特稱,則結(jié)論為特稱。特稱命題即為含“有的”的之言命題,如“有的學(xué)生是黨員”就是一個特稱命題。
例如,“有的學(xué)生是黨員”和“有的學(xué)生是大學(xué)生”并不能推出任何結(jié)論;而“有的動物是魚”和“所有魚都生活在水里”,只能推出“有的動物生活在水里”這一特稱命題。
(2)一否得否:兩個前提不能都是否定命題,且只要前提有一個為否定,則結(jié)論為否定。
例如,“所有學(xué)生都不是志愿者”和“小李不是學(xué)生”并不能推出任何結(jié)論;而“所有學(xué)生都不是志愿者”和“小李是志愿者”,只能推出“小李不是學(xué)生”這一否定命題。
三、復(fù)言命題
復(fù)言命題是由兩個或多個單句通過聯(lián)結(jié)詞聯(lián)結(jié)而成的命題。根據(jù)邏輯聯(lián)結(jié)詞的不同,可以將復(fù)言命題劃分為聯(lián)言命題、選言命題和假言命題。
(1)聯(lián)言命題:聯(lián)言命題就是將若干個命題聯(lián)合起來,表示這些情況同時存在的命題。日常聯(lián)言命題的邏輯聯(lián)結(jié)詞還有“是…也是…”、“不僅…還…”、“…同時…”等。
可表示為:p并且q(p、q是聯(lián)言肢,“并且”是聯(lián)結(jié)詞)。
聯(lián)言命題的推理規(guī)則為“一假即假,全真才真”,具體解釋為:
1.全部肢命題為真推出聯(lián)言命題為真;
2.其中有一個肢命題為假,那么聯(lián)言命題就為假。
例如: “小李是中國人”和“小李是學(xué)生”同時為真時才可以推出“小李是中國人且小李是學(xué)生”這一命題。
(2)選言命題:選言命題就是給出若干個命題,可以選擇出一種或者多種情況存在的命題。根據(jù)所能選擇的情況不同,可以分為兩種:
1. 相容選言命題:多種情況可以同時存在。可表示為:p或者q(p、q是選言肢,“或者”是聯(lián)結(jié)詞)。其真假關(guān)系為“一真即真,全假才假”。
2. 不相容選言命題:只允許一種情況存在。可表示為:要么p,要么q(p、q是選言肢,“要么……要么……”是聯(lián)結(jié)詞)。其真假關(guān)系為“同真同假為假,一真一假為真”。
選言命題的推理規(guī)則可以通過以下表格來表示:
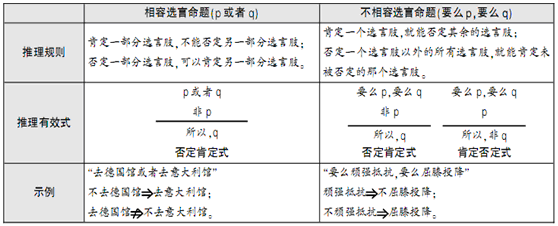
(3)假言命題:假言命題就是帶有假設(shè)條件的命題。假言命題通常包含兩個肢命題:反映條件的肢命題在前,稱為前件;反映結(jié)果的肢命題在后,稱為后件。根據(jù)前后件間條件關(guān)系的不同,又可分為三種:
1. 充分條件假言命題:當(dāng)條件p存在時,結(jié)論q一定成立,而無需考慮其他條件,則p是q的充分條件,即“有它就行”。可表示為:如果p,那么q或p→q(p是前件,q是后件,“如果……那么……”是聯(lián)結(jié)詞)。其推理規(guī)則為“肯前肯后,否后否前;肯后不肯前,否前不否后”。
2. 必要條件假言命題:當(dāng)條件p不存在時,結(jié)論q一定不成立,則p是q的必要條件。即“沒它不行”。可表示為:只有p,才q或p←q(p是前件,q是后件,“只有……才……”是聯(lián)結(jié)詞)。其推理規(guī)則為“否前否后,肯后肯前;肯前不肯后,否后不否前”。
3. 充分必要條件假言命題:表示p是q的充分條件和必要條件的命題,即表示p與q等值的命題。可表示為:p當(dāng)且僅當(dāng)q(p是前件,q是后件,“當(dāng)且僅當(dāng)”是聯(lián)結(jié)詞)。其推理規(guī)則為“肯前肯后,否前否后;肯后肯前,否后否前”。
四、模態(tài)命題
模態(tài)命題即含有“必然”、“可能”等模態(tài)詞的命題。模態(tài)命題主要存在兩組矛盾,即“必然p”與“可能非p”、“必然非p”與“可能p”。如“今天必然是晴天”與“今天可能不是晴天”是一組矛盾關(guān)系,“今天必然不下雨”與“今天可能下雨”是一組矛盾關(guān)系。
否定模態(tài)命題,即在命題前加否定詞,得到其矛盾命題,
并非“必然p”=“可能非p”,即不必然=可能不;
并非“必然非p”=“可能p”,即不必然不=可能;
并非“可能p”=“必然非p”,即不可能=必然不
并非“可能非p”=“必然p”,即不可能不=必然

